Force, Net Force, and Acceleration

What causes acceleration?

What is a vector?

In the Motion Sensor Labs, you did a variety of experiments where the low-friction car was moving, sometimes at a constant velocity and sometimes with changing velocity. Obviously, when the car was moving with a constant velocity, its acceleration was zero, and when the car had changing velocity, its acceleration was NOT zero.

What causes acceleration?  Under what conditions does an object accelerate and under what conditions will an object NOT accelerate?

To answer these questions, let’s look at some of the experiments from the two Motion Sensor Labs.

Figure 5,The p-t graph for the fan car experiment is shown above.

Figure 1, The air-track experiment involved pushing the glider, then LETTING GO.

In this experiment, there are three forces acting on the car:  the weight of the car, the force of the track pushing up, and the force from the fan pushing the car to the right.  These forces are all shown as vectors (the arrows) on the diagram.  As with the case of the glider, the weight of the car and the force of the track pushing up cancel each other out.  But this time instead of there being zero net force, there is an unbalanced force, the force of the fan.  This fan force is unbalanced because there is no other force in the opposite direction to cancel it out.  The car does have a net force acting on it.  The net force is equal to the force of the fan to the right.

In the case where there is an unbalanced force acting on the car (there is a net force), what kind of motion does the car have?  First, look at the p-t graph in your lab book from this experiment.  You will find that the graph you collected looks much like the one below.

In the air-track experiment, you pushed the glider then LET GO.  The glider traveled down the air-track with essentially no friction (the glider was floating on air!).  Refer back to your lab book and notice that the p-t graph recorded by the motion sensor looked like the graph below.

Figure 2, The p-t graph for the flat air-track experiment is shown above. Remember in that experiment you pushed the glider then let go.

In this experiment, as the graph above shows, the glider moved with constant velocity after you stopped pushing.  Only the data for the times after you stopped pushing are plotted in Figure 2.  The slope of the line on the p-t graph is constant (straight line), so the velocity of the glider was constant and the acceleration was zero.  What are the conditions that cause this uniform motion (constant velocity)?  Click here to see the v-t graph from this experiment.

After you let go of the glider, what forces were acting on it?  Remember your hand is no longer pushing on the glider!  Can you push on an object without touching it?  The answer is no, unless you are Luke Skywalker or Harry Potter.  What forces ARE pushing or pulling on the glider?  With no friction, the only forces are the glider’s own weight pulling it down and the force of the air coming out of the track that pushes the glider up.  The weight of any object is a force (so it is also measured in Newtons), because weight is defined as the force the gravity of the earth (or another large object) exerts on an object with a certain mass or, in other words, the weight of an object is how much the earth pulls it down toward the ground.  The diagram shown below is called a Free Body Diagram of these forces. 

The data is only plotted for the times AFTER you let go of the glider.

Weight of the Glider Pulling it Down  (Fg)

Force of the Air Pushing the Glider Up  (FAir)

Figure 3,   A Free Body Diagram of the forces pushing and pulling on the glider after you let go is shown above.

How do you think the force of the air pushing up on the glider and the glider’s weight pulling down compare?  These forces have the same amount of force but in opposite directions, so they cancel each other out. The amount of force is called the magnitude and the arrows that show both the direction and magnitude of the force are called vectors. Click here for a definition of vectors.  If the force of the air was more than its weight, the glider would start to move upwards.  If the glider’s weight was more than the force of the air pushing up, then the glider would start to move downwards.  Since the glider does not move up or down, its weight and the force of the air must be equal and cancel each other out.

There is nothing touching the glider that could push or pull it in the horizontal direction.  It is important to remember that objects cannot put forces on each other unless they touch each other.  The only exceptions are the weird cases of gravity (e.g. the Earth can pull on you without touching you), magnets, and static- electrical forces.  I am not sure which one of these weird forces Luke Skywalker uses.

In the case of the glider, there are no horizontal forces acting on the glider and the only two vertical forces cancel each other out.  This situation is referred to as zero net force.  When the glider has zero net force, what kind of motion does it display?  It moves with constant velocity (no acceleration).  So keep these two states linked in your mind: 

When an object has no forces acting on it (no or zero net force), the object moves with constant velocity (no acceleration).              (Statement-1)

But what happens to an object when forces do act on it (or, more precisely, when unbalanced forces act on the object)?  This question sounds like the one addressed in the motion sensor experiment on the flat-track where the fan was attached to the car. 

Figure 4,   The car on the flat track with fan pushing it to the right is shown above.

Weight of the Car Pulling it Down  (Fg)

Force of the Track Pushing the Car Up  (FT)

Force of the Fan

pushing the car                                 right (Ff)

In this graph for the fan-car experiment, the slope of the line is changing (a curved line), so the velocity is changing.  This interpretation means the car is accelerating (speeding up, in this case).  To see the v-t graph from this experiment, click here.

What if the Force Opposes the

Direction of Motion?

What happens when the net force on an object is in the opposite direction that the object is moving?  You have also experimented with this situation. In the motion-sensor lab, you had a car set up with a fan pushing on the car towards the left, but you gave the car an initial large push (with your hand) to the right, as shown below.

Figure 6,   The car on flat track is moving to the right with the fan pushing it to the left.

Weight of the Car Pulling it Down  (Fg)

Force of the Track Pushing the Car Up  (FT)

Force of the Fan

pushing left (Ff)

The car is moving to the right, because of your initial push.

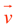
The red arrow shows the initial velocity vector. The car moves to the right, because of the initial push you gave the car.  The velocity vector contains two pieces of information:  (1) the direction the object is moving and (2)  the speed it is moving with (represented by the length of the vector).  The force vectors are shown on the free body diagram (FBD) in black.  This diagram is drawn for a time after you let go (stopped pushing) the car.  The only forces on the car at this point in time are the weight of the car, the force of the track, and the force of the fan. The first two forces cancel each other out, as with the other experiments.  The force of the fan is unbalanced and in the opposite direction of  the motion (or velocity vector), so the net force is to the left, but the motion is to the right.  What happens?

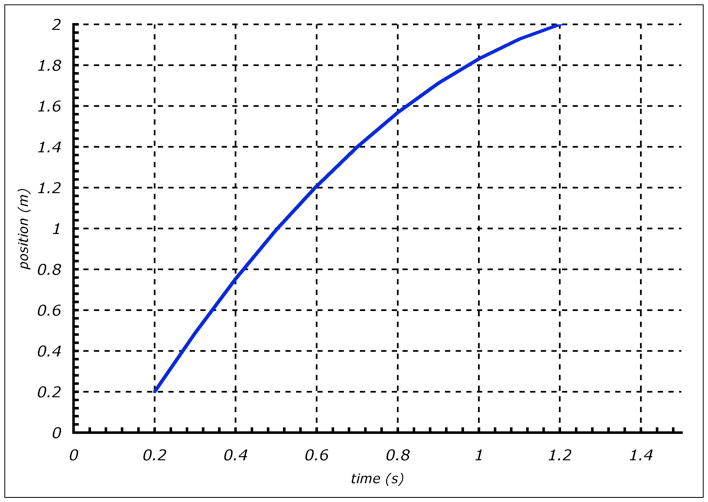
Figure 7,   The p-t graph for a car on a flat-track moving to the right with a fan pushing it to the left is shown above.

The p-t graph above should be similar to the one you obtained in the experiment.  The slope of the curve starts very steep, corresponding to the relatively large initial velocity.  As time passes, the slope becomes more shallow, which means the velocity is decreasing.  An object slows down when it is moving and a force is applied to it in the opposite direction of its motion.

Once again, we are faced with an unbalanced force (net force present) causing a change in velocity (acceleration).  But in this case, the acceleration results in a decrease in velocity.

What determines the direction of acceleration?

Thus far we have assumed that the glider and the car were moving in the positive direction.  We could just as easily have run the experiments with the car or glider moving in the negative direction.  Remember that it is always your decision as to how to set up the number line that defines the positions.  For instance, Figure 8 below shows the number line set up as it was in the experiments we have talked about so far.  The car moves in the positive direction (toward +∞), because of the way the number line is set up.  On the other hand, Figure 9 shows an alternate way to set up the number line so the car is moving in the negative direction (toward -∞).

Figure 8,   This diagram shows a car on a flat-track moving in the positive direction (right) and being pushed by fan to the left, after you let go.

Weight of the Car Pulling it Down  (Fg)

Force of the Track Pushing the Car Up  (FT)

Force of the Fan

pushing left (Ff)

The car is moving to the right, because of your initial push.

Figure 9,   After you let go, a car on a flat-track moves in the negative direction (right) and is pushed by the fan to the left.

Weight of the Car Pulling it Down  (Fg)

Force of the Track Pushing the Car Up  (FT)

Force of the Fan

pushing left (Ff)

The car is moving to the right, because of your initial push.

By simply changing our number line, we can redefine which direction is + (positive) and which is - (negative).

Notice in Figure 8, the car moves in the + direction, but the force from the fan is in the - direction.  This means the acceleration is also negative (acceleration is defined to always have the same direction, or sign, as the net force).  In Figure 8, the velocity is +, the acceleration is -, and the car slows down. 

On the other hand, notice in Figure 9, the car moves in the - direction, but the force from the fan is in the + direction.  This means the acceleration is also positive.  In Figure 9, the velocity is -, the acceleration is +, and the car slows down.  In other words, when the velocity and acceleration are in opposite directions (or have opposite signs), the object slows down. 

However, if the velocity is in the + direction and the net force and, therefore, acceleration is in the + direction, the object should speed up.  The object would also speed up if the object is moving in the - direction and the applied net force and acceleration is in the - direction.  When the velocity of the object and the force are in the same direction (or they have the same sign), the object speeds up.

A summary of these conclusions are shown in the table below.  For a video demo of an accelerometer to help explain these conclusions, click here. 

Copyright  © 2009-2012, by Marcus Milling

edited by Julia Pian

When an unbalanced force is acting on an object, its velocity changes. 

In other words, its motion is not uniform and the object is

accelerating.                                                                      

(Statement-2)

So force causes acceleration.  Statement 1 and 2 above are two of the most important conclusions from all of physics.  Without understanding these two physical truths, we would never have sent people to the Moon or spacecraft to Mars.